El álgebra Booleana
Ustedes se preguntaran qué es el álgebra Booleana "es un sistema matemático
deductivo centrado en los valores cero y uno (falso y verdadero). Un operador
binario “ º “ definido en éste juego de valores acepta un par de entradas y
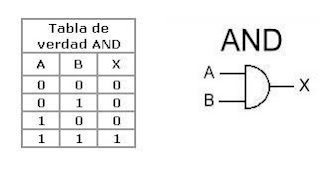
produce un solo valor booleano, por ejemplo, el operador booleano AND acepta
dos entradas booleanas y produce una sola salida booleana.
Para cualquier sistema algebraico existen una serie de postulados iniciales, de aquí se pueden deducir reglas adicionales, teoremas y otras propiedades del sistema, el álgebra booleana a menudo emplea los siguientes postulados:
• Cerrado. El sistema booleano se considera cerrado con respecto a un operador binario si para cada par de valores booleanos se produce un solo resultado booleano.
• Conmutativo. Se dice que un operador binario “ º “ es conmutativo si A º B = B º A para todos los posibles valores de A y B.
• Asociativo. Se dice que un operador binario “ º “ es asociativo si (A º B) º C = A º (B º C) para todos los valores booleanos A, B, y C.
• Distributivo. Dos operadores binarios “ º “ y “ % “ son distributivos si A º (B % C) = (A º B) % (A º C) para todos los valores booleanos A, B, y C.
• Identidad. Un valor booleano I se dice que es un elemento de identidad con respecto a un operador binario “ º “ si A º I = A.
• Inverso. Un valor booleano I es un elemento inverso con respecto a un operador booleano “ º “ si A º I = B, y B es diferente de A, es decir, B es el valor opuesto de A.
Para nuestros propósitos basaremos el álgebra booleana en el siguiente juego de operadores y valores:
- Los dos posibles valores en el sistema booleano son cero y uno, a menudo llamaremos a éstos valores respectivamente como falso y verdadero.
- El símbolo • representa la operación lógica AND. Cuando se utilicen nombres de variables de una sola letra se eliminará el símbolo •, por lo tanto AB representa la operación lógica AND entre las variables A y B, a esto también le llamamos el producto entre A y B.
- El símbolo “+” representa la operación lógica OR, decimos que A+B es la operación lógica OR entre A y B, también llamada la suma de A y B.
- El complemento lógico, negación ó NOT es un operador unitario, en éste texto utilizaremos el símbolo “ ‘ “ para denotar la negación lógica, por ejemplo, A’ denota la operación lógica NOT de A.
- Si varios operadores diferentes aparecen en una sola expresión booleana, el resultado de la expresión depende de la procedencia de los operadores, la cual es de mayor a menor, paréntesis, operador lógico NOT, operador lógico AND y operador lógico OR. Tanto el operador lógico AND como el OR son asociativos por la izquierda.
Si dos operadores con la misma procedencia están adyacentes, entonces se evalúan de izquierda a derecha. El operador lógico NOT es asociativo por la derecha."
Para más información consulta aquí.
Leyes de Morgan
Las Proposiciones
"Una proposición es una afirmación que puede recibir un valor de verdad falso (F), o bien verdadero (V), pero no ambos a la vez.
Su denotación generalmente la encontramos con las letras (p, q, r)
Conectores Lógicos
Podemos formar nuevas proposiciones a partir proposiciones dadas mediante el uso de conectivos lógicos. Algunos de ellos son:
^ “y” conjunción
v “o” disyunción
-> “si —, entonces” implicación
<-> “si y sólo si” doble implicación
¬ “no” negación
Leyes de Morgan
Son una parte de la Lógica proposicional, analítica ,y fueron creada por Augustus de Morgan.
Estas declaran las reglas de equivalencia en las que se muestran que dos proposiciones pueden ser lógicamente equivalentes.
Las Leyes de Morgan permiten:
El cambio del operador de conjunción en operador de disyunción y viceversa.
Las proposiciones conjuntivas o disyuntivas a las que se aplican las leyes de Morgan pueden estar afirmadas o negadas (en todo o en sus partes).
Casos:
¬(P ^ Q) ≡ (¬P v ¬Q)
Si nos encontramos con una proposición conjuntiva totalmente negada, la ley de Morgan nos permite transformarla en una proposición disyuntiva con cada uno de su miembros negados
¬(P v Q) ≡ (¬P ^ ¬Q)
Si nos encontramos con una proposición disyuntiva totalmente negada, la ley de Morgan nos permite transformarla en una proposición conjuntiva con cada uno de sus miembros negados
(P ^ Q) ≡ ¬ (¬ P v ¬ Q)
Si nos encontramos con una proposición conjuntiva afirmada, la ley de Morgan nos permite transformarla en una proposición disyuntiva negada en su totalidad y en sus miembros.
(P v Q) ≡ ¬(¬P ^ ¬Q)
Si nos encontramos con una proposición disyuntiva afirmada, la ley de Morgan nos permite transformarla en una proposición conjuntiva negada en su totalidad y en sus miembros."
Mapas de Karnaugh
¿Qué son los mapas de Karnaugh?
"Otra manera de simplificar funciones es representándolas en
mapas de Karnaugh. Esto es equivalente a resolver las simplificaciones por
teoremas. Sin embargo, mucha gente considera que resulta más fácil visualizar
las simplificaciones si se presentan gráficamente.
Ejemplo 1: Simplifica la función de dos variables f = a'b + ab' + ab
Lo primero que debo de hacer es representarlo en un mapa de dos variables. Se representa como una tabla. Para llenar la tabla, pongo un uno donde se intersecte el valor de la función. Por ejemplo, para el primer término de la función f = a'b + ab' + ab, se ha marcado en rojo donde se puso el 1 en la tabla.
Una vez hecho el mapa, debemos marcar las regiones contiguas que manejen 1s. Aquí en el dibujo vemos cómo se marcan dos regiones. Estas regiones son las simplificaciones. Como la región azul involucra solamente a la b, eso representa. La región verde, por su parte, involucra solamente a la a. Para cada región, debemos verificar qué variables involucra. En el caso de la región azul, cubre a la b, pero con respecto a la variable a maneja tanto a como a', y por eso se descarta la a. Una vez definidas las regiones, se escribe la función simplificada f= b + a."